I’m at Bath Ruby 2015, live blogging some of the talks
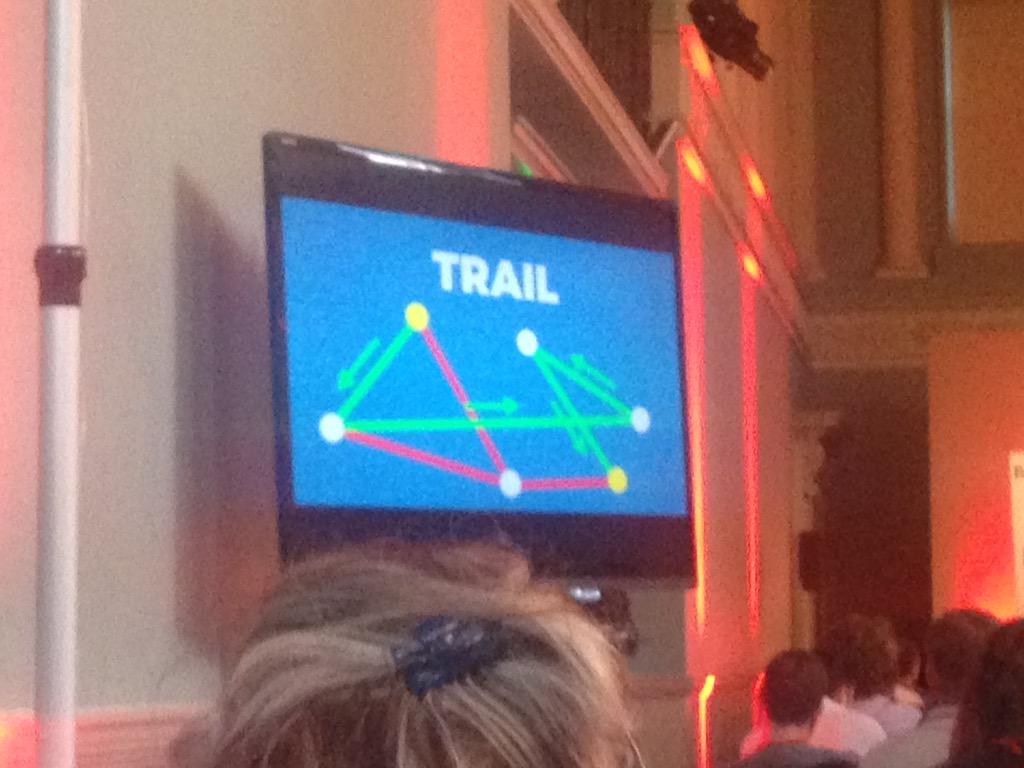
Photo by @trailsuite
- Brains are just not very good at working with several complex ideas concurrently
- Abstraction is our solution to this
- Numbers are a property of sets (?) of things. It doesn’t matter how we arrange the things, or how big they are
- We build other concepts on top of our idea of number: e.g. successor - a way to generate new numbers. gt/lt can be built from the idea of successors
- These abstractions allow us to predict what would happen in reality when certain actions occur: we can do the ‘work’ in the ‘abstract world’ rather than doing it in the real world and observing the result.
- Recognise patterns. Some patterns can be generalised to apply to whole classes of items (e.g. all natural numbers)
- You don’t need to remember the details of why a particular formula works: it doesn’t matter: you can use it without understanding why it’s true
- A walk across a graph is a sequence of visits from node to node along their adjacent edges
- A connected graph is one where there exists a walk between any pair of notes
- A trail is a walk which doesn’t repeat traversing edges
- An Euleurian trail is a walk which visits every node and uses every edge
- Mathematics: “spot patterns, build reusable abstractions”
- Abstractions help us take complex things from the real world and reconstruct them in our heads so that we cal (?reason about them?)
- Idea of the honest abstraction - the one which ‘honestly’ models your problem.
- The minimal abstraction: start from nothing and only add the behaviours/ideas/operations which are strictly necessary
- “the most exciting thing you can do with your brain is to strap it into the hulking exoskeleton of mathematics”
- If you can write a program, you’re good at mathematics